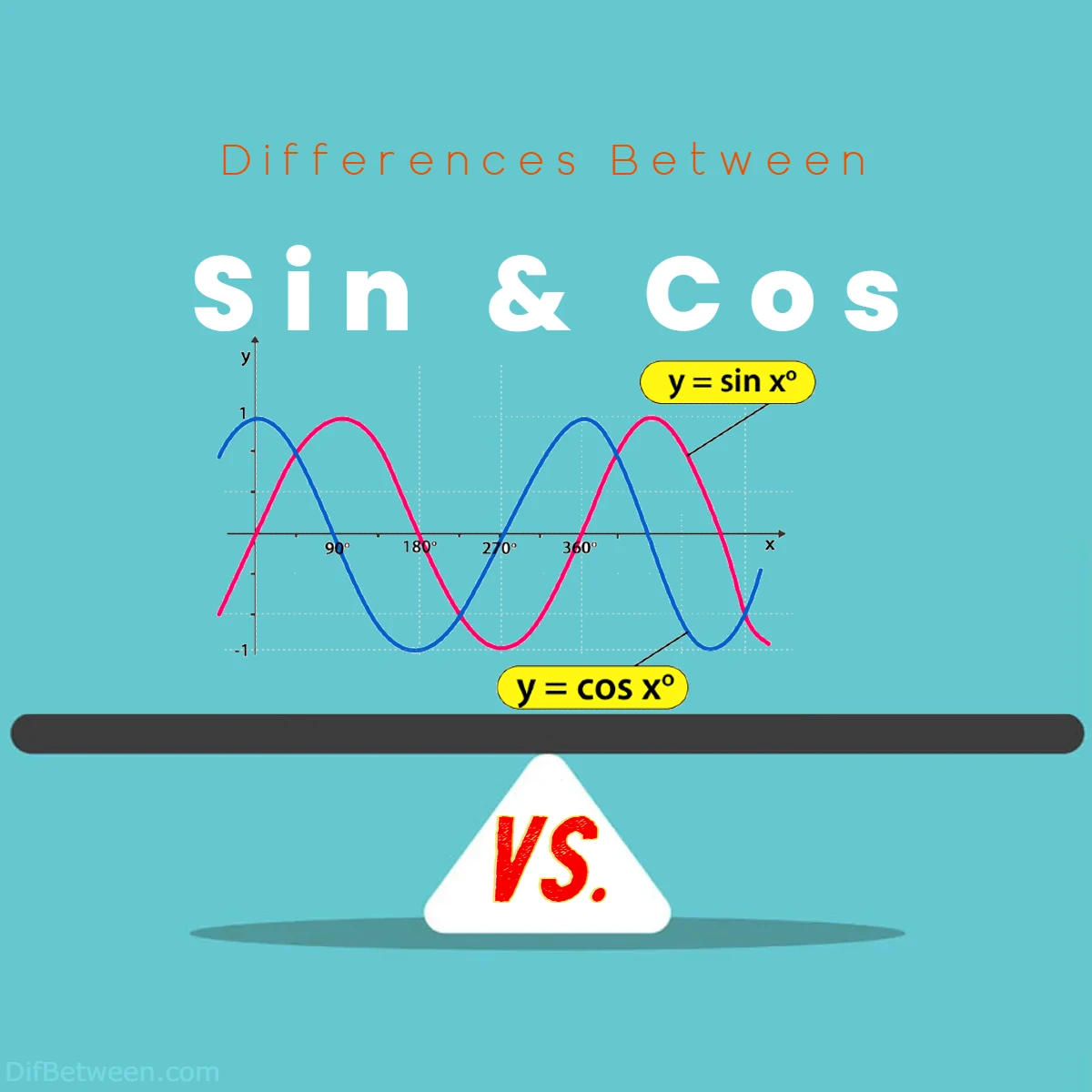
The main differences between sine (sin) and cosine (cos) lie in their graphical behavior and starting points on the unit circle. Sine functions produce an oscillatory wave-like pattern, commencing at zero, reaching peaks, descending to troughs, and repeating. On the other hand, cosine functions exhibit a similar wave pattern but initiate at their peak, then descend to troughs, rise to peaks, and repeat. Essentially, the distinction arises in their phase relationship, with the sine function starting at zero, while the cosine function begins at its peak. These disparities are pivotal in trigonometry, influencing applications in physics, engineering, and signal processing.
| Aspect | Sine Function (sin) | Cosine Function (cos) |
|---|---|---|
| Definition | sin(θ) = opposite/hypotenuse | cos(θ) = adjacent/hypotenuse |
| Graphical Behavior | Oscillatory wave-like pattern, starts at zero, peaks, descends to trough, and repeats. | Similar wave-like pattern but starts at peak, descends to trough, rises to peak, and repeats. |
| Amplitude | Constant amplitude of 1 | Variable amplitude, affected by vertical shifts |
| Real-world Applications | Simple harmonic motion, AC circuits | Physics scenarios with phase shifts, signal processing |
| Trigonometric Identities | Reciprocal identity: csc(θ) = 1/sin(θ)<br> Pythagorean identity: sin²(θ) + cos²(θ) = 1 | Reciprocal identity: sec(θ) = 1/cos(θ)<br> Pythagorean identity: 1 + tan²(θ) = sec²(θ) |
| Phase Shifts | Phase shift of π/2 radians or 90 degrees with respect to each other. sin(θ) = cos(θ – π/2), cos(θ) = sin(θ + π/2) | No phase shift between the functions |
| Symmetry | Odd function, symmetry about the origin | Even function, symmetry about the y-axis |
| Integration | ∫sin(θ) dθ = -cos(θ) + C<br> ∫cos(θ) dθ = sin(θ) + C | ∫cos(θ) dθ = sin(θ) + C<br> ∫sin(θ) dθ = -cos(θ) + C |
| Differentiation | d/dθ sin(θ) = cos(θ)<br> d/dθ cos(θ) = -sin(θ) | d/dθ cos(θ) = -sin(θ)<br> d/dθ sin(θ) = cos(θ) |
| Frequency and Periodicity | Both have the same frequency and a period of 2π radians or 360 degrees. | Both exhibit periodic behavior with the same frequency and period. |
| Euler’s Formula | e^(iθ) = i*sin(θ) | e^(iθ) = cos(θ) |
| Practical Considerations | Suitable for scenarios involving vertical motion or oscillation. | Suitable for scenarios where motion begins at an extreme position. |
Delving into the Basics
Let’s embark on a journey through the realm of trigonometry, where the sine (sin) and cosine (cos) functions take center stage. Both these mathematical functions are pivotal in describing the relationships between angles and sides in a right-angled triangle. Before we explore their differences, let’s grasp the fundamental definitions.
Sine (sin): The sine of an angle in a right-angled triangle is the ratio of the length of the side opposite the angle to the length of the hypotenuse. In mathematical terms, if θ is an angle in a right triangle, then sin(θ) = opposite/hypotenuse.
Cosine (cos): Similarly, the cosine of an angle is the ratio of the length of the adjacent side to the length of the hypotenuse. For an angle θ, cos(θ) = adjacent/hypotenuse.
Unveiling the Differences
Geometric Perspective
When we visualize the sine and cosine functions graphically, a key distinction emerges. The sine function is renowned for its oscillatory nature, producing a wave-like pattern. Its graph starts at zero, rises to a peak, descends through zero to a trough, and repeats this cycle indefinitely. On the other hand, the cosine function, though fundamentally similar, exhibits a slight phase shift. The cosine wave begins at its peak, descends through zero to a trough, and then rises to peak again.
| Sine Function (sin) | Cosine Function (cos) | |
|---|---|---|
| Peak | Starts at zero, rises to peak, descends to trough, and repeats. | Starts at peak, descends to trough, rises to peak, and repeats. |
| Initial Value | sin(0) = 0 | cos(0) = 1 |
| Amplitude | 1 | 1 |
Understanding these geometric distinctions lays the foundation for comprehending their applications in various mathematical and scientific domains.
Application in Real-world Scenarios
The sine and cosine functions find diverse applications beyond the confines of trigonometry textbooks. Engineers, physicists, and scientists harness these functions to model and analyze periodic phenomena.
Sine Function (sin): One of the classic applications of the sine function is in describing simple harmonic motion. From the oscillation of a pendulum to the vibrations of a guitar string, sine waves encapsulate the essence of periodicity. Additionally, sine functions play a crucial role in electrical engineering, especially in alternating current (AC) circuits.
Cosine Function (cos): While cosine shares similarities with the sine function, its applications often manifest in scenarios where phase shifts matter. In physics, cosine functions might represent situations where the initial state begins at a peak or trough. Moreover, cosine functions are prevalent in signal processing and control systems, where the alignment of different waveforms is a critical consideration.
Trigonometric Identities
Delving deeper into the intricacies of trigonometry, we encounter a web of interrelated identities. Both sine and cosine contribute significantly to these identities, forming the backbone of trigonometric manipulations.
| Sine Function (sin) | Cosine Function (cos) | |
|---|---|---|
| Reciprocal Identity | csc(θ) = 1/sin(θ) | sec(θ) = 1/cos(θ) |
| Pythagorean Identity | sin²(θ) + cos²(θ) = 1 | 1 + tan²(θ) = sec²(θ) |
These identities showcase the symbiotic relationship between sine and cosine, each contributing to the elegance and versatility of trigonometric manipulations.
Phase Shifts and Symmetry
Examining the functions from a mathematical standpoint, we encounter nuanced differences related to phase shifts and symmetry.
Phase Shifts: Sine and cosine functions exhibit a phase shift of π/2 radians or 90 degrees with respect to each other. This means that the sine of an angle is equal to the cosine of that angle minus π/2, and vice versa. Mathematically, sin(θ) = cos(θ – π/2) and cos(θ) = sin(θ + π/2).
Symmetry: The cosine function is an even function, showcasing symmetry about the y-axis. In contrast, the sine function is an odd function, displaying symmetry about the origin. This intrinsic dissimilarity contributes to the diverse ways these functions manifest in mathematical expressions and graphical representations.
Behavior at Key Angles
As we traverse the unit circle, exploring the behavior of sine and cosine at key angles provides valuable insights.
| Angle (θ) | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| sin(θ) | 0 | 1/2 | √2/2 | √3/2 | 1 |
| cos(θ) | 1 | √3/2 | √2/2 | 1/2 | 0 |
These values serve as reference points, aiding in quick calculations and providing a glimpse into the oscillatory nature of sine and cosine functions.
Graphical Representations and Amplitude
Digging deeper into the graphical representations of sine and cosine functions, another key difference lies in their amplitude.
Amplitude: The amplitude of a wave is the measure from the peak (or trough) to the center line of the wave. In both sine and cosine functions, the amplitude is 1. However, while the sine function maintains a consistent amplitude throughout, the cosine function’s amplitude is susceptible to vertical shifts.
| Sine Function (sin) | Cosine Function (cos) | |
|---|---|---|
| Amplitude | 1 | Variable (affected by vertical shifts) |
Understanding this distinction aids in accurately interpreting and manipulating sine and cosine graphs in diverse mathematical contexts.
Integration and Differentiation
Venturing into calculus, the study of integrals and derivatives unveils further insights into the disparities between sine and cosine.
Integration: When integrating sine and cosine functions, a notable difference arises in the sign of the result. The integral of sin(θ) with respect to θ yields -cos(θ), and the integral of cos(θ) results in sin(θ). This sign alternation emphasizes the complementary nature of these functions.
Differentiation: Derivatives showcase another facet of the relationship between sine and cosine. The derivative of sin(θ) is cos(θ), and the derivative of cos(θ) is -sin(θ). Once again, this interplay of signs underscores the intricate dance between these fundamental trigonometric functions.
Frequency and Periodicity
While both sine and cosine functions exhibit periodic behavior, they differ in their interpretation of frequency and the concept of periodicity.
Frequency: In the context of periodic functions, frequency refers to the number of cycles completed in a unit interval. For sine and cosine functions, the frequency is identical, emphasizing their shared oscillatory nature.
Periodicity: The period of a function is the smallest positive number T for which f(θ + T) = f(θ) for all θ. Both sine and cosine functions have a period of 2π radians or 360 degrees. This means that the functions repeat their values every 2π radians, forming the basis for their periodicity.
Complex Numbers and Euler’s Formula
Introducing the realm of complex numbers elevates our understanding of sine and cosine functions through Euler’s formula.
Euler’s Formula: Euler’s formula establishes a profound connection between trigonometric functions, complex numbers, and exponential functions. It states that for any real number θ, e^(iθ) = cos(θ) + i*sin(θ), where i is the imaginary unit. This formula beautifully encapsulates the essence of sine and cosine functions within the realm of complex numbers.
| Sine Function (sin) | Cosine Function (cos) | |
|---|---|---|
| Euler’s Formula | e^(iθ) = i*sin(θ) | e^(iθ) = cos(θ) |
Understanding the implications of Euler’s formula provides a powerful tool for expressing trigonometric functions in the language of complex analysis.
Practical Considerations in Calculations
In practical applications, the choice between using sine or cosine functions often depends on the specifics of the problem at hand.
Sine Function (sin): Sine functions are frequently employed when dealing with problems involving vertical motion or oscillation. The sine function’s inherent starting point at zero aligns with scenarios where the motion initiates from the equilibrium position.
Cosine Function (cos): Conversely, cosine functions find favor in situations where the motion begins at an extreme position. The cosine function’s starting point at the peak or trough aligns seamlessly with scenarios where the object is displaced from its equilibrium position.
Final Thoughts
As we unravel the intricate tapestry of trigonometry, the differences between sine and cosine functions emerge as more than mere oscillations on a graph. From their geometric nuances to their role in calculus and complex analysis, sine and cosine functions stand as pillars of mathematical understanding. Whether you are navigating waves on a string, deciphering electrical currents, or delving into the elegance of complex numbers, the symbiotic dance between sine and cosine enriches our mathematical landscape. As we conclude this exploration, may the sinuous curves of sine and cosine continue to guide and inspire the curious minds traversing the realms of mathematics.
FAQs
The fundamental difference lies in their graphical behavior and starting points. The sine function produces an oscillatory wave starting at zero, reaching peaks and troughs, while the cosine function exhibits a similar wave pattern but starts at its peak, descending to troughs, rising to peaks, and repeating.
Sine functions are often employed to model simple harmonic motion and alternating current circuits, where their starting point aligns with equilibrium positions. In contrast, cosine functions find utility in scenarios with phase shifts, prevalent in physics and control systems, as their starting point corresponds to extreme positions.
Yes, there are symmetry differences. The sine function is odd and symmetric about the origin, while the cosine function is even and symmetric about the y-axis. This characteristic impacts their graphical representations and mathematical manipulations.
The integration and differentiation of sine and cosine functions result in sign alternations. The integral of sin(θ) is -cos(θ), and the integral of cos(θ) is sin(θ). Similarly, the derivatives of sin(θ) and cos(θ) are cos(θ) and -sin(θ), respectively.
Yes, both functions share the same frequency and periodicity. They complete one full cycle every 2π radians or 360 degrees, making them essential components in describing periodic phenomena.
Sine and cosine functions have a phase shift of π/2 radians or 90 degrees with respect to each other. This means that the sine of an angle is equal to the cosine of that angle minus π/2, and vice versa.
Yes, Euler’s formula establishes a connection between trigonometric functions and complex numbers. For the sine function, e^(iθ) = i*sin(θ), while for the cosine function, e^(iθ) = cos(θ). Euler’s formula provides a powerful tool for expressing sine and cosine in the language of complex analysis.
Read More: